
Ohio University chemist explains an old question with a modern tool

Ohio University chemist Jixin Chen, Ph.D., took advantage of the time when labs were shut down early in the pandemic to apply a very modern solution to solve a very old question.
Like Joseph Fourier did 200 years ago, Chen sat down with paper and pen to look at diffusion, which is a fundamental process in nature that controls the speed of things happening, known as kinetics, in systems such as the transportation of materials in a living cell and human body, catalysis in chemical industry, batteries, corrosion in oil pipes, pollution dynamics, and electron transportations in metal wires and microchips.
Albert Einstein and George Stokes were able to connect Adolf Fick's Laws of diffusion and Robert Brown’s observations of Brownian motion a century ago with their "drunken sailor" theory. But when Chen applied some modern tools to the task—running computer simulations using the computer language MATLAB—he was able for the first time to explain a connection between discrete and continuous interpretations of diffusive adsorption.
Chen is an associate professor of chemistry and biochemistry in the College of Arts and Sciences at Ohio University, and he recently published his work on "Simulating stochastic adsorption of diluted solute molecules at interfaces" in AIP Advances.
How and when does a particle get from point A to point B?
Usually, diffusion and flow are the two main ways of materials transportation. The diffusive transportation of a substance was described early on using mathematical equations such as Fick’s law of diffusion at the macroscopic and ensemble level, and later researchers added descriptions of random walk, or motion at single-molecule or particle level.
"However, there is a problem between these two interpretations," Chen said. "The diffusion has a fractal nature which is difficult to justify and understand in the models (Figure 1 left). That is, when a particle moves from location A to B in a period over time (∆t), it travels many places which are very different from just moving from A to B in the shortest path. Rather, it is a self-similar process traveling from one place to another if one zooms in time."
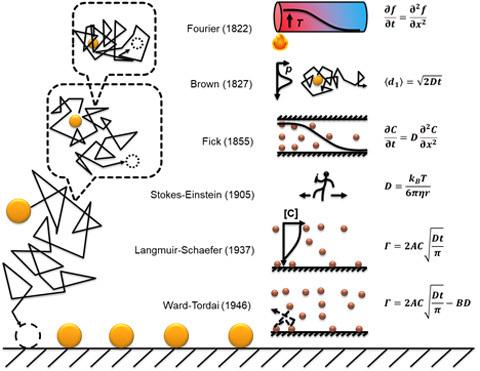
Historically (Figure 1), Fick summarized two laws from Fourier (a paper published in 1822) and Brown’s work (in 1827) on diffusion and Brownian motion with the connection of a parameter called the diffusion constant (in 1855). Stokes and Einstein connect the diffusion constant at a single particle level to the bulk properties of the substances using a random walk model (in 1905). This theory is well known as the “drunken sailor” problem. With these developments, Langmuir and Schaefer came up with an equation to predict the adsorption kinetics of diluted molecules onto a surface (in 1937). The model assumes that all molecules that hit the surface are adsorbed, which is further corrected by Ward and Tordai (in 1946) by introducing a rejection term when not all molecules are adsorbed.
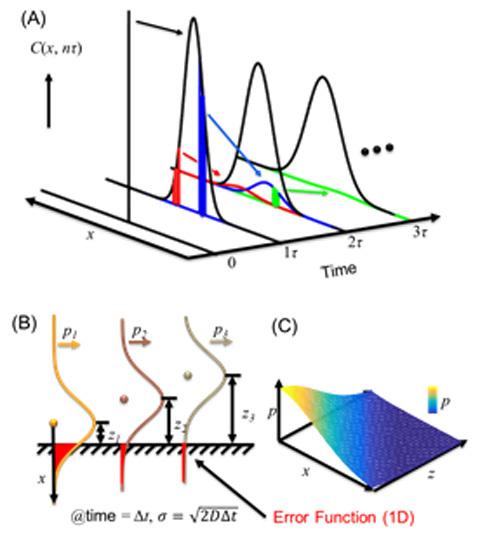
"A very popular way to understand the adsorption is through the discrete random walk model as Einstein did," Chen said. "Assuming you drop an ink drop into the water, the ink molecules diffuse and the drop spreads out over time with a nice Gaussian distribution shown in Figure 2. Thus the probability over space of seeing any molecule at time t is represented by the black curves. To calculate the probability of molecules adsorbing to a surface placed in a uniform bulk solution, like coffee adsorbing to a spoon placed in a cup of coffee, we just add up all error functions shown in Figure 2B. This simple argument makes a lot of sense and is typically used in computer simulations when a discrete-time step is selected. However, this simple argument has two folds of difference than the results predicted by the Langmuir-Schaefer equation and often orders of magnitude difference from the experimental results."
Using Monte Carlo simulations to close the gap between Brownian motion and drunken sailor models
Chen’s recent article tries to close the gap between these differences using computer Monte Carlo simulations, which can model different outcomes with random variable. He discovered that the two-fold difference between the discrete simulations and the Langmuir-Schaefer equation comes from the fractal nature of the diffusion. That is, each diffusion probability function is composed of a series of self-similar but smaller probability functions (Figure 1 left and figure 2A).
"When we ignore this detail, we remove the sub-step diffusion and introduce an error," he said. "To add back the fractal diffusion, one has to simulate the diffusion at over 1,000 times finer in time than the time of interest, or simply add back a correction term manually using the Cauchy series in the Zeno’s paradoxes, that is 1+1/2+1/4+… = 2. The several order of magnitude difference between experiments and theory is due to the uncertainty of the sub-surface concentration gradient evolved during the adsorption. That is, the molecule near the surface is depleted over time and it takes time for the bulk molecules to diffuse to the sub-surface to refill the 'vacuum' which is a chaotic process in experiments, just like we have never seen a perfect Gaussian profile when we drop a drop of ink into water."
Chen is also a member of the Nanoscale Quantum Phenomena Institute (NQPI) at Ohio University.
