Jixin Chen discovers new reaction rate in solution, with implications for industrial, biological processes

While the world watches the FIFA soccer world cup, chemist Jixin Chen and his students are studying another kind of "ball" and discovering that a 100-year-old collision theory doesn't stand up to 21st century calculations.
A shot on goal in a soccer game involves pretty simple geometry—the speed, distance traveled, and trajectory of the ball as it collides with the goalie or the net.
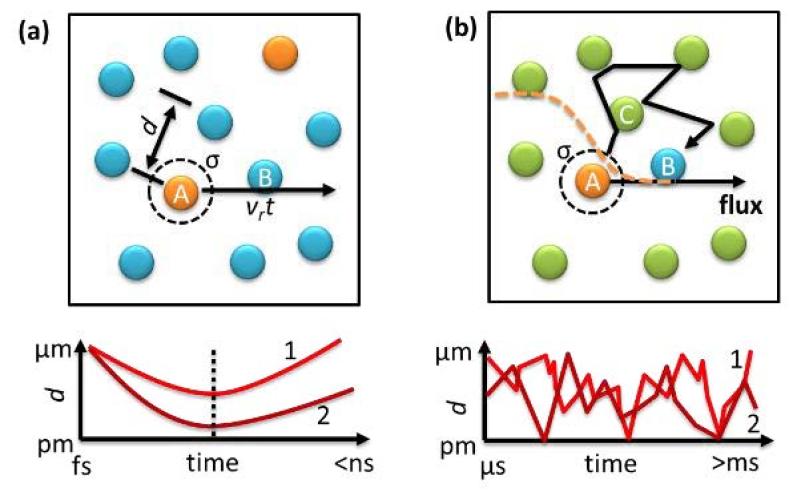
The Chen lab illustrates its new discovery on the rate of chemical reactions with a thought experiment that looks like a soccer game with a lot of balls (subbing in for molecules) and geometric collisions (Figure 1a). But as Chen explains, things get complicated (Figure 1b) when that ball game is happening in a state of diffusion—almost too big for today's supercomputers to handle. Almost.
“The diffusion theory has been a struggle for the greatest scientists including Albert Einstein and Richard Feynman for a long time. It has taken me over 10 years to learn what they have derived and extended a tiny step in this paper for a particular problem,” said Chen, associate professor of chemistry and biochemistry in the College of Arts and Sciences, and a member of Ohio University Nanoscale and Quantum Phenomena Institute.

Why revising the collision theory is necessary
Chen's lab studies kinetics, which involves measuring and studying the rates of reactions. Predicting the reaction kinetics, i.e. how fast a reaction can happen in a solution, is essential information for many processes, such as industrial chemical manufacturing, refining, synthesis and separation of petroleum products, environmental processes in air and water, biological reactions in cells, bio-sensing, and drug delivery.
Chen discusses his new findings in an article on "Why the Reaction Order of a Bimolecular Reaction Should be 2.33 instead of 2?" in the Journal of Physical Chemistry A.
"Collision theory, which uses a lot of geometry, was originally developed to explain the reaction kinetics of gas reactions with no dilution. But for a reaction in a diluted inert gas solution or a diluted liquid solution, diffusion often dominates the collision process, so we have to include diffusion in our calculations," Chen said.
"Updating the calculations on collision frequency with diffusion is essential to us. There are more relevant problems of reactions that happened in the diluted conditions than in the neat gas phase, such as reactions in all biological systems, in the ocean, in the air, or in most industrial processes," he said.
Calculating reactions at a nanosecond time scale vs a second scale
Chen noted that rate of reaction and energy distribution theories developed by J.C. Maxwell and Ludwig Boltzmann in the 19th century left a problem unsolved in predicting a reaction rate—how to calculate frequency and the activation energy of the reaction. A possible solution—collision theory—developed by Max Trautz and William Lewis in the early 20th century has been successful in explaining the reaction kinetics in the gas phase when there is no dilution. Smoluchowski during the same period developed an equation to calculate the collision rate at the long-time limit assuming a steady diffusion flux has established near the molecules.
But Chen's article discusses a different collision model that is derived from the adsorption of molecules on a flat surface. In the soccer analogy, adsorption (adhesion of molecules to a surface) might be akin to a soccer player's sweat sticking to the ball in a header and causing a slightly different deflection than if the soccer player was not sweaty.
"A surprising result is obtained showing that the reaction order for bimolecular reaction should be 2 + 1/3 instead of 2, following a fractal reaction kinetics," he said. "The basic idea is that for two molecules, one can calculate their collision frequency using models such as a simple hard sphere collision model, and then calculate the reaction probabilities of all possible collision geometries."
In the classical collision theory, the collision frequency is calculated from the randomly oriented speeds of the molecules, v, that are Maxwell-Boltzmann distributed, the density of the molecules, and the cross-section of the collisions. "It is like the probability of randomly shooting a ball to a matrix of balls," Chen said, "and the time to hit one is proportional to the distance of the space divided by the speed.
"The average distance of the free of the fly before hitting a ball is called the mean free path. Typically, you would expect to hit a ball within nanoseconds of fly under normal conditions (for gasses), with a mean free path of ~80 nanometers and an average speed of ~500 meters per second for a small molecule like oxygen. The collision frequency is dependent on the product of the concentrations of the two molecules, as many scientists including Richard Feynman have explained in their lectures. The probability of the reaction of each collision can be calculated using the transition state theory either classically or quantum mechanically. It focuses on the collision geometry near the dashed line in Figure 1a, when two molecules approach each other and calculate the activation energy and collision geometry needed to break old chemical bonds and form new bonds," Chen writes in the journal article.
"However, there is still a gap in knowledge of collision theory nowadays. When an inert molecule C is introduced as a solvent to dilute the molecules and form a solution, the time scale for the collision between the molecules of interest and the distance time trajectory (Figure 1b) looks very different than the scenario Figure 1a illustrates. There are no clear trajectories for the collisions and the simple argument on time of fly fails. The frequency of finding the other molecules now is controlled by diffusion, and it becomes one of the dominating steps for the reaction kinetics that may takes seconds," Chen concludes.
This diffusion process has been historically described by many models such as the “drunken sailor” random walk model proposed by scientists including Albert Einstein. Nowadays, this process is usually studied using molecular dynamic simulations. However, there is a technical difficulty for the dynamic simulation to predict the reaction kinetics. When the molecule is too diluted, for example, it will take milliseconds for a collision of interest to happen which is challenging the computational power of current computers.
Classically, the two cases shown in Fig. 1 share similar rate equations with a reaction order of 2, with Figure 1b as the diffusive collision case. But the dependence of collision frequency on the concentrations of the reactants of these two cases should be different," Chen said.
"If we look at the single-molecule level, the distance of fly is proportional to the time of fly (<x> = vrt), and the time of diffusion is square dependent on the distance (<x2>=2Drt). Thus, the two rate equations are very unlikely to have the same dependence on the average molecular distance that is determined by the concentrations."
The bottom line, Chen said, is that "complications have been observed in simulations and experiments that are challenging the foundation of this rate equation in the reaction order of 2."
Chen’s research has been partially supported by NIH NHGRI grant 1R15HG009972 (https://reporter.nih.gov/project-details/9440801) managed by program officer Dr. Michael Smith (https://www.genome.gov/staff/Michael-W-Smith-PhD). The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
